AIAG-VDA PFMEA製程失效模式與效應分析
了解新發佈AIAG-VDA PFMEA製程失效模式與效應分析的差異與要求
■了解新發佈AIAG-VDA PFMEA製程失效模式與效應分析的差異與要求。 ■了解如何有效地將現有AIAG FMEA(第四版)調整到新版的模式。 ■了解新版AIAG-VDA PFMEA的更新與維護。


|
將提供新版AIAG-VDA FMEA與
舊版FMEA(第四版)差異與應用重點說明,不容錯過!!
[新版PFMEA效益]
■了解新發佈AIAG-VDA PFMEA製程失效模式與效應分析的差異與要求。
■了解如何有效地將現有AIAG FMEA(第四版)調整到新版的模式。
■了解新版AIAG-VDA PFMEA的更新與維護。
[課程目標]
■充分了解『新版AIAG-VDA PFMEA』的要求及重點項目。
■課程訓練注重製程PFMEA實務說明、進行詳細案例練習與解說。
■透過課程中雙向溝通,加強學習效果。
[課程大綱]
一、新版AIAG-VDA FMEA基礎介紹
1. 新舊版變化主要差異說明
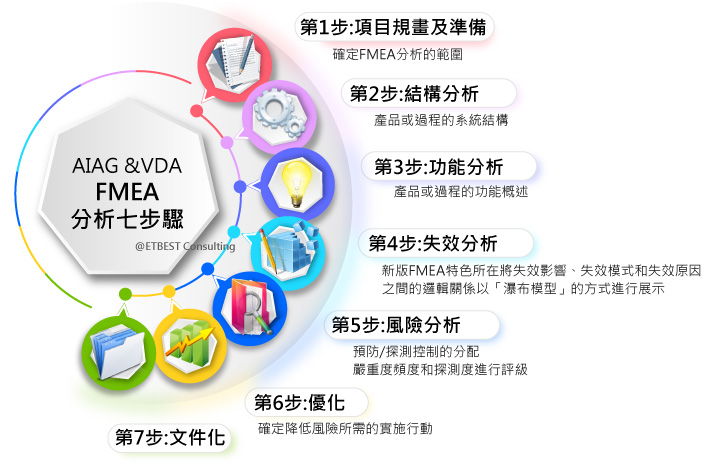
2. 分析七步驟之應用時機與重點要求
二、製程PFMEA的七步驟
1. 步驟一 規劃和準備
2. 步驟二 結構分析
3. 步驟三 功能分析
4. 步驟四 失效分析
5. 步驟五 風險分析
6. 步驟六 優化
7. 步驟七 結果文件化
※各步驟案例練習與討論
三、PFMEA & CP管制計畫的聯接
四、分享與討論Q&A
五、課程測驗
[防疫公告]
- 因應武漢肺炎防疫,進入易騰企管教室時敬請配合:
1、自行準備與配戴口罩。
2、自備飲用水杯。
3、量測額溫。(超過37℃請勿進入)
4、手部酒精消毒。
5、填寫健康聲明 。
- 若有以下情況之一者,請暫時不要參加本次課程:
1、開課前14天內有任何出國史,或者
2、有咳嗽、呼吸急促、發燒等感冒症狀。
感謝您的配合,易騰企管與您攜手守護健康
1.課程費用含稅、課程教材、上課證明、午餐、點心、茶水供應…等(半天課程恕未提供午餐)
2.優惠折扣:同公司二人同行9折,三人以上同行85折優惠。
【付款方式有三種】
================
1.匯款:
戶名:易騰國際股份有限公司
統一編號:12690254
銀行名稱:華南銀行-竹北分行
帳號:323-10-0003769
銀行代號:008-3238。
2.支票:請於開課前郵寄支票,支票抬頭請開「易騰國際股份有限公司」
3.上課現場繳納
●其他說明
1.已報名者若有異動,請於開課前一天告知;未提早一天通知而未到課者,
將停止本公司提供折扣與優惠三個月 ; 若使用免費人天,將視同使用。
2.易騰企管保留開課日期&授課講師變更之權利,請依易騰最新課程公告為準。
報名諮詢
報名方式:
1. 點選亞太教育訓練網下方之「我要報名」按鈕進而填寫報名資訊即可。
2. 或電洽:02-27363878 *521 張小姐、02-27363878 *136 黃小姐。
※注意事項※ 為確保您的上課權益,報名後若未收到任何回覆,請來電洽詢方可完成報名
1.易騰企管專用訓練教室【新竹縣竹北市嘉豐南路二段76號6F-2】
●課程費用
易騰企業管理顧問成立於2000年6月。公司成立的宗旨在於突破企業管理顧問的發展瓶頸,堅持提供高品質與高附加價值的顧問服務與專業課程。透過先進的網路技術與客戶互動溝通,不斷的提升服務的內容以及拉近與客戶的距離。 ... more










